Зі шкільних уроків геометрії багато хто пам’ятає, що трикутник — це фігура з трьома кутами та трьома сторонами. Але коли доходить до практичних завдань, як-от розрахунок матеріалів для ремонту чи просто допомога дитині з домашнім завданням, питання «як знайти площу трикутника?» може збити з пантелику. На щастя, це не так складно, як здається.
Насправді існує кілька способів обчислити площу цієї простої фігури, і вибір методу залежить від того, які дані у вас є. У цій статті ми розберемо найпоширеніші та найкорисніші формули, які допоможуть вам легко впоратися з будь-яким трикутником.
Класичний спосіб: через основу та висоту
Це найвідоміша і, мабуть, найпростіша формула, яку вивчають у школі. Вона універсальна і підходить для будь-якого типу трикутника.
Формула: S = (1/2) * a * h
Де:
- S — це площа трикутника.
- a — довжина однієї зі сторін трикутника, яку ми називаємо основою.
- h — висота, тобто перпендикуляр, проведений з протилежної вершини до цієї основи.
Як це працює на практиці?
Уявіть, що у вас є трикутник, де довжина основи становить 10 см, а висота, проведена до неї, — 6 см.
- Перемножуємо довжину основи на висоту: 10 см * 6 см = 60 см².
- Ділимо отриманий результат на два: 60 см² / 2 = 30 см².
Площа нашого трикутника — 30 квадратних сантиметрів. Все просто! Головна складність тут — знайти або виміряти висоту, що не завжди можливо.
Для прямокутного трикутника: ще простіше
Якщо ваш трикутник має прямий кут (90°), завдання значно спрощується. Вам не потрібно шукати висоту, адже її роль виконує одна зі сторін.
Формула: S = (1/2) * a * b
Де a і b — це катети, тобто сторони, що утворюють прямий кут.
По суті, прямокутний трикутник — це половина прямокутника. Тому, щоб знайти його площу, достатньо перемножити довжини катетів і поділити на два.
Приклад:
Катети трикутника дорівнюють 5 см і 8 см.
Площа S = (5 см * 8 см) / 2 = 40 см² / 2 = 20 см².
Коли відомі всі сторони: формула Герона
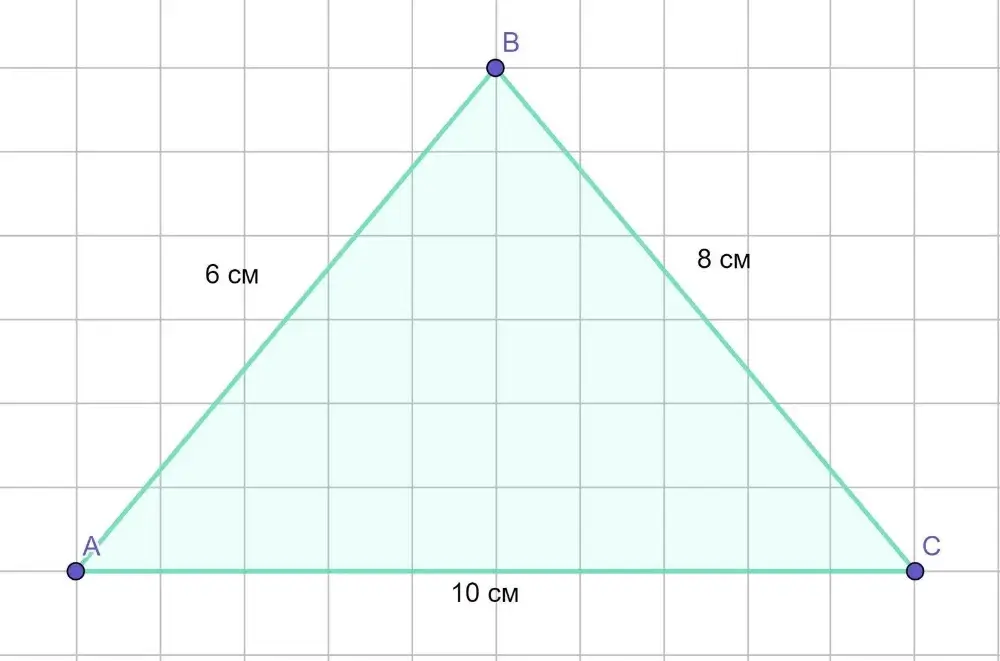
А що робити, якщо висота невідома, але ви знаєте довжини всіх трьох сторін? На допомогу приходить античний математик Герон Олександрійський та його елегантна формула. Вона виглядає трохи складніше, але є надзвичайно корисною.
Формула: S = √[p * (p – a) * (p – b) * (p – c)]
Тут з’являється нова змінна:
- a, b, c — довжини трьох сторін трикутника.
- p — це півпериметр, тобто половина суми всіх сторін: p = (a + b + c) / 2.
- √ — знак квадратного кореня.
Давайте розберемо на прикладі:
У нас є трикутник зі сторонами 13 см, 14 см і 15 см.
- Знаходимо півпериметр (p):
p = (13 + 14 + 15) / 2 = 42 / 2 = 21 см. - Підставляємо значення у формулу:
S = √[21 * (21 – 13) * (21 – 14) * (21 – 15)]
S = √[21 * 8 * 7 * 6]
S = √7056 - Обчислюємо квадратний корінь:
S = 84 см².
Формула Герона — справжній рятівник, коли інші методи застосувати неможливо.
Якщо відомі дві сторони і кут між ними
Цей метод часто використовується в тригонометрії. Якщо ви знаєте довжини двох сторін і величину кута, що лежить між ними, знайти площу також нескладно.
Формула: S = (1/2) * a * b * sin(α)
Де:
- a, b — довжини двох відомих сторін.
- sin(α) — синус кута (α) між цими сторонами.
Для обчислення синуса можна скористатися калькулятором. Цей спосіб ідеально підходить для розв’язання задач, де фігурують кути.
Таблиця: який метод обрати?
Щоб вам було легше орієнтуватися, ми зібрали всі методи в одну таблицю.
| Відомі дані | Яку формулу використовувати | Примітки |
|---|---|---|
| Сторона і висота | S = (1/2) * a * h | Універсальний та найпростіший метод. |
| Два катети | S = (1/2) * a * b | Лише для прямокутних трикутників. |
| Три сторони | Формула Герона | Ідеально, коли висота невідома. |
| Дві сторони і кут | S = (1/2) * a * b * sin(α) | Потрібен калькулятор для синуса. |
Розуміння, а не зазубрювання
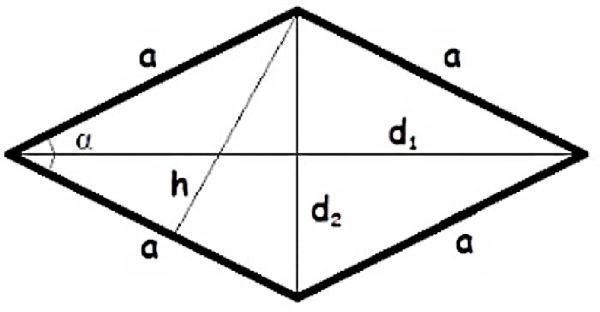
Знання формул — це важливо, але ще важливіше розуміти логіку, яка за ними стоїть. По суті, будь-який трикутник можна розглядати як половину відповідного паралелограма (або прямокутника у випадку з прямокутним трикутником). Саме тому в багатьох формулах присутнє ділення на два.
Розуміння цих простих принципів допоможе вам не просто запам’ятати формули, а й застосовувати їх усвідомлено, легко знаходячи площу трикутника в будь-якій ситуації — чи то на іспиті, чи під час планування ремонту у власній оселі.