Геометрія часто здається складною, але багато її завдань мають прості та логічні рішення. Одне з таких завдань — знаходження площі трапеції. Ця фігура зустрічається не тільки в шкільних підручниках, але й у реальному житті: у архітектурі, дизайні, будівництві та навіть при розрахунку площі земельних ділянок. Розуміння, як обчислити її площу, є корисною практичною навичкою.
Давайте розберемося в основних формулах та методах, які допоможуть вам легко впоратися з цим завданням, навіть якщо ви давно закінчили школу.
Що таке трапеція та її ключові елементи
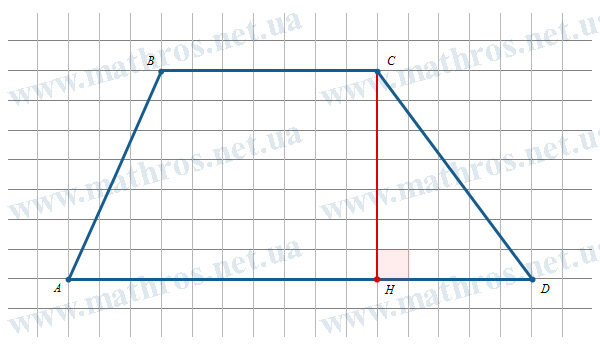
Перш ніж переходити до формул, згадаймо, що таке трапеція. Це чотирикутник, у якого дві сторони паралельні, а дві інші — ні.
- Основи (a, b): Це ті самі дві паралельні сторони. Та, що довша, називається нижньою основою, а коротша — верхньою.
- Бічні сторони (c, d): Дві непаралельні сторони. Якщо вони рівні, трапеція називається рівнобічною.
- Висота (h): Це перпендикуляр, проведений з будь-якої точки однієї основи до іншої. Висота завжди однакова по всій довжині трапеції.
Саме ці елементи є ключовими для більшості розрахунків.
Основна формула площі трапеції
Найпростіший і найпоширеніший спосіб знайти площу трапеції — це використати її основи та висоту. Формула виглядає так:
S = (a + b) / 2 * h
Де:
- S — площа трапеції.
- a і b — довжини основ.
- h — висота.
По суті, ми знаходимо середнє арифметичне довжин основ (це ще називають середньою лінією трапеції) і множимо його на висоту.
Приклад задачі:
Уявімо, що у нас є трапеція з верхньою основою a = 6 см, нижньою основою b = 10 см і висотою h = 5 см.
- Спочатку додаємо довжини основ: 6 + 10 = 16 см.
- Ділимо суму на 2: 16 / 2 = 8 см.
- Множимо отримане значення на висоту: 8 * 5 = 40 см².
Отже, площа нашої трапеції дорівнює 40 квадратних сантиметрів.
Цей метод є універсальним і підходить для будь-якого типу трапеції, чи то прямокутної, чи рівнобічної.
Як знайти площу, якщо висота невідома?
Часто в умовах задачі висота не дається прямо. У такому випадку її потрібно знайти, використовуючи інші властивості фігури, найчастіше — теорему Піфагора. Це особливо актуально для рівнобічної трапеції.
Кроки для знаходження висоти в рівнобічній трапеції:
- Проведіть дві висоти з вершин верхньої основи до нижньої. Вони відітнуть від трапеції два однакових прямокутних трикутники.
- Знайдіть довжину катета одного з цих трикутників. Він дорівнюватиме: (b – a) / 2.
- Знаючи цей катет і бічну сторону (яка є гіпотенузою), знайдіть висоту (другий катет) за теоремою Піфагора: h = √(c² – ((b – a) / 2)²).
Після того як ви знайшли висоту, можна повертатися до основної формули обчислення площі.
Інші методи обчислення площі
Існують і менш поширені, але корисні формули, які можуть знадобитися за наявності інших даних.
Через діагоналі
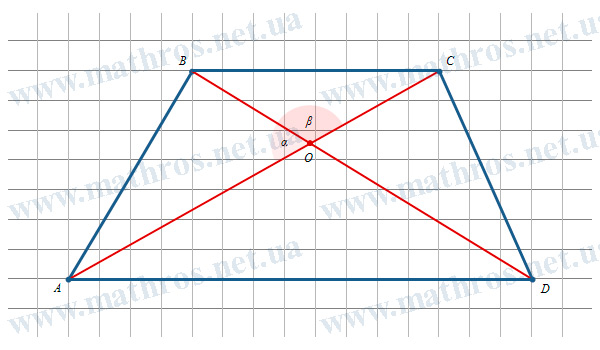
Якщо ви знаєте довжини діагоналей (d₁, d₂) та кут (α) між ними, площу можна знайти так:
S = (d₁ * d₂) * sin(α) / 2
Цей метод зручний, коли виміряти висоту складно, але можна легко визначити параметри діагоналей.
| Метод | Необхідні дані | Формула |
|---|---|---|
| Основний | Дві основи (a, b) та висота (h) | S = ((a + b) / 2) * h |
| Через середню лінію | Середня лінія (m) та висота (h) | S = m * h |
| Через діагоналі | Дві діагоналі (d₁, d₂) та кут між ними (α) | S = (d₁ * d₂) * sin(α) / 2 |
Практичне застосування знань
Навички обчислення площі трапеції можуть стати в пригоді в найнесподіваніших ситуаціях. Наприклад, при ремонті кімнати з трапецієподібною стіною, при розкрої тканини або при плануванні ландшафтного дизайну на ділянці неправильної форми.
Знання базових геометричних формул не лише допомагає розв’язувати абстрактні задачі, а й дає змогу ефективніше вирішувати практичні питання. Як бачите, знайти площу трапеції зовсім не складно, якщо знати правильний підхід і розуміти логіку, що стоїть за формулами.