Геометрія часто здається складною, але багато завдань стають простими, якщо розуміти основні принципи. Ромб — одна з тих геометричних фігур, площу якої можна знайти кількома зручними способами. Незалежно від того, чи допомагаєте ви дитині з домашнім завданням, чи просто освіжаєте знання, ця стаття допоможе вам розібратися з усіма тонкощами обчислення площі ромба.
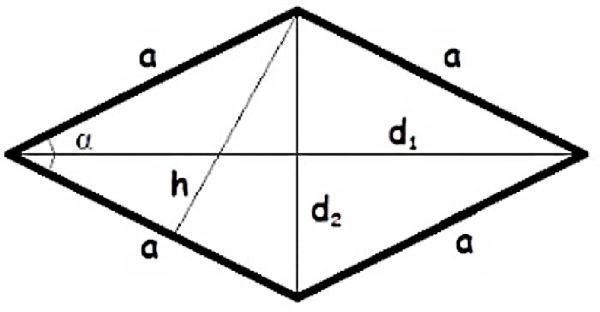
Для початку згадаймо, що таке ромб. Це паралелограм, у якого всі чотири сторони рівні. Ця проста властивість і визначає унікальні методи для розрахунків.
Спосіб 1: Через діагоналі — найпопулярніший метод

Найчастіше для обчислення площі ромба використовують його діагоналі. Це відрізки, що з’єднують протилежні вершини фігури. Важливо пам’ятати ключові властивості ромба, пов’язані з ними: діагоналі ромба завжди перетинаються під прямим кутом (90°) і в точці перетину діляться навпіл.
Формула площі ромба через діагоналі виглядає так:
S = (d1 * d2) / 2
де:
- S — площа ромба;
- d1 — довжина першої діагоналі;
- d2 — довжина другої діагоналі.
Тобто, щоб знайти площу, потрібно перемножити довжини діагоналей і поділити результат на два.
Приклад:
Уявімо, що в нас є ромб, діагоналі якого дорівнюють 8 см та 6 см.
S = (8 * 6) / 2 = 48 / 2 = 24 см².
Площа цього ромба становить 24 квадратних сантиметри. Просто, чи не так?
Спосіб 2: Через сторону та висоту
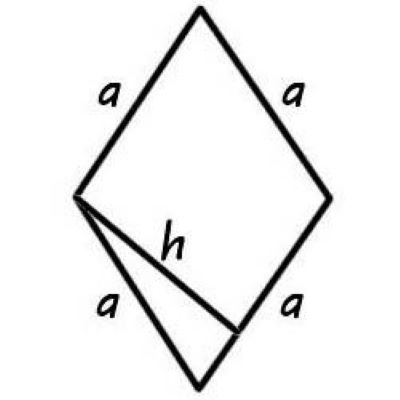
Оскільки ромб є різновидом паралелограма, для нього можна застосувати й загальну формулу площі паралелограма. Для цього нам знадобиться довжина сторони та висота, проведена до цієї сторони. Висота — це перпендикуляр, опущений з будь-якої вершини на протилежну сторону.
Формула обчислення площі в цьому випадку:
S = a * h
де:
- a — довжина сторони ромба;
- h — довжина висоти, проведеної до цієї сторони.
Цей метод зручний, якщо діагоналі невідомі, але є дані про сторону та висоту.
Порада: Важливо не плутати висоту з діагоналлю. Висота завжди утворює прямий кут зі стороною, на яку вона опущена, тоді як діагональ з’єднує протилежні кути.
Спосіб 3: Через сторону та кут

Що робити, якщо відома лише довжина сторони та один із кутів ромба? І для такого випадку існує своя формула. Вона базується на тригонометрії, але не лякайтеся, все досить просто.
Формула площі ромба через сторону та синус кута між сторонами:
S = a² * sin(α)
де:
- a — довжина сторони;
- sin(α) — синус кута між двома суміжними сторонами ромба.
Варто пам’ятати, що протилежні кути ромба рівні, а сума сусідніх кутів завжди дорівнює 180°. Тому не має значення, синус якого з кутів ви використовуєте — гострого чи тупого, результат буде однаковим.
Приклад:
Нехай сторона ромба дорівнює 10 см, а гострий кут між сторонами становить 30°.
Значення sin(30°) дорівнює 0,5.
S = 10² * sin(30°) = 100 * 0,5 = 50 см².
Отже, площа ромба — 50 квадратних сантиметрів.
Яку формулу обрати для обчислення площі?
Вибір методу залежить виключно від того, які дані у вас є. Підсумуємо в зручній таблиці:
| Відомі дані | Рекомендована формула |
|---|---|
| Довжини двох діагоналей (d1, d2) | S = (d1 * d2) / 2 |
| Довжина сторони (a) та висоти (h) | S = a * h |
| Довжина сторони (a) та кут між ними (α) | S = a² * sin(α) |
Розуміння цих трьох підходів дає змогу впевнено розв’язувати більшість задач, пов’язаних із площею ромба.
Практичне застосування знань
На перший погляд, пошук площі геометричних фігур може здатися абстрактною вправою. Проте ці навички корисні в реальному житті: в ремонті (розрахунок кількості плитки чи паркету для укладання ромбовидним візерунком), у дизайні, архітектурі та навіть у деяких видах рукоділля. Знання базових формул робить нас більш впевненими у вирішенні повсякденних практичних завдань. Тож тепер ви точно знаєте, як підійти до цієї фігури з будь-якого боку.