Уміння знаходити площу прямокутника — це не просто шкільна навичка. Вона стає у пригоді в найрізноманітніших життєвих ситуаціях: від планування ремонту та розрахунку кількості матеріалів до облаштування саду чи навіть вирішення логічних завдань. Здавалося б, що може бути простіше, ніж помножити дві сторони? Але навіть у цьому питанні є свої нюанси та цікаві підходи, які допоможуть вам впоратися з будь-яким завданням.
Цей матеріал допоможе вам не лише пригадати основну формулу, а й зрозуміти, як діяти в нестандартних ситуаціях, коли відомі, наприклад, лише діагональ і одна зі сторін. Ми розберемо все на простих прикладах, щоб ви могли легко застосувати ці знання на практиці.
Що таке прямокутник і його основні властивості
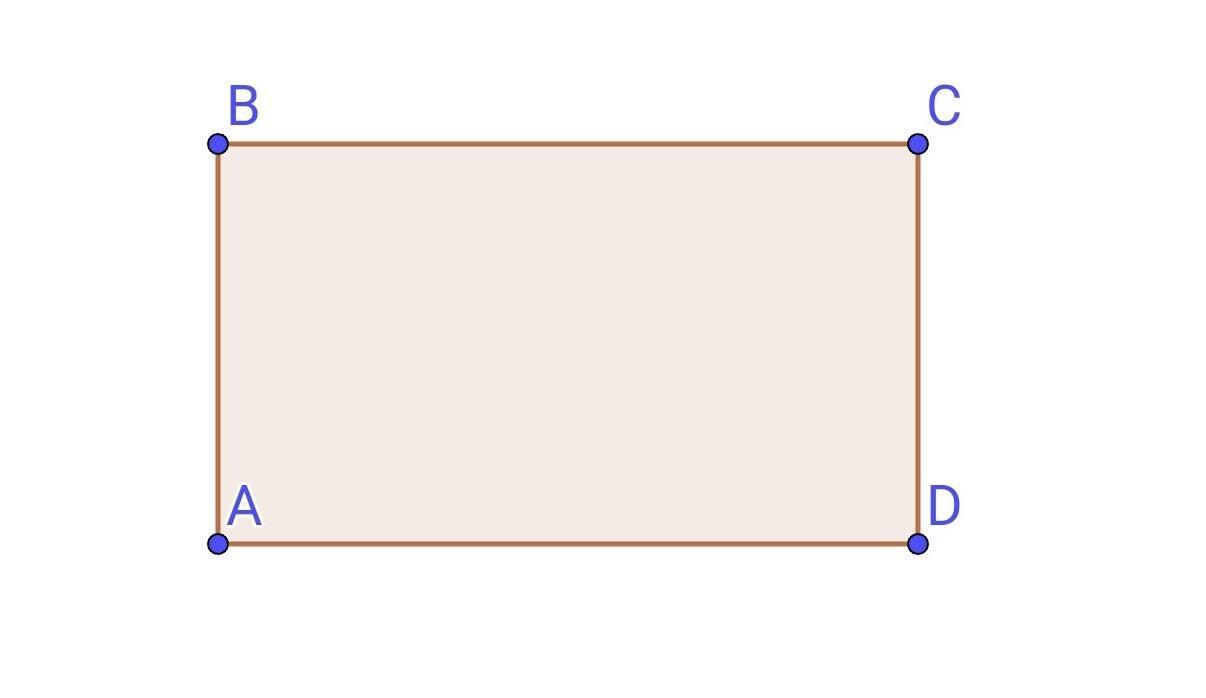
Перш ніж занурюватися в розрахунки, давайте коротко пригадаємо, що таке прямокутник. Це чотирикутник, у якого всі кути прямі (по 90 градусів), а протилежні сторони рівні та паралельні між собою.
Основні властивості, які важливо пам’ятати:
- Протилежні сторони рівні: якщо одна довжина дорівнює 10 см, то й протилежна їй сторона також має 10 см.
- Усі кути прямі: це ключова характеристика, яка відрізняє його від, наприклад, паралелограма.
- Діагоналі рівні: вони перетинаються в одній точці та діляться нею навпіл.
Розуміння цих властивостей є основою для всіх подальших обчислень, включно з пошуком площі.
Класична формула площі прямокутника
Найбільш відомий і простий спосіб обчислити площу (S) прямокутника — це помножити його довжину (a) на ширину (b).
Формула виглядає так:
S = a × b
де:
- S — площа фігури;
- a — довжина однієї сторони;
- b — довжина суміжної сторони (ширина).
Результат вимірюється у квадратних одиницях: квадратних метрах (м²), сантиметрах (см²) тощо, залежно від одиниць вимірювання сторін.
Порада: Завжди перевіряйте, щоб обидві сторони були виміряні в однакових одиницях. Якщо довжина в метрах, а ширина в сантиметрах, спочатку приведіть їх до єдиної системи вимірювання, інакше результат буде неправильним.
Приклад простого розрахунку
Уявімо, що вам потрібно пофарбувати стіну, довжина якої 5 метрів, а висота — 3 метри. Щоб зрозуміти, скільки фарби купувати, потрібно знати площу стіни.
- a = 5 м
- b = 3 м
- S = 5 м × 3 м = 15 м²
Отже, площа стіни становить 15 квадратних метрів.
Як знайти площу, коли відомі інші дані
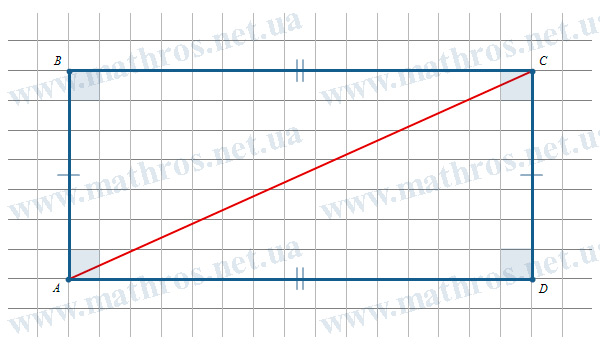
Іноді умови задачі не дають нам довжину та ширину напряму. Розглянемо кілька популярних сценаріїв та методи їх вирішення.
Обчислення через діагональ і одну сторону
Уявіть, що ви знаєте довжину діагоналі (d) та однієї зі сторін (a). Як знайти площу? Тут на допомогу приходить теорема Піфагора. Діагональ ділить прямокутник на два однакові прямокутні трикутники, де діагональ є гіпотенузою, а сторони — катетами.
Формула для знаходження невідомої сторони (b) буде такою:
b = √(d² – a²)
Знайшовши другу сторону, ви можете використати класичну формулу площі S = a × b.
Приклад:
Діагональ екрана монітора дорівнює 13 дюймам, а його ширина — 5 дюймам. Знайдемо площу екрана.
- Знаходимо невідому сторону (висоту):
b = √(13² – 5²) = √(169 – 25) = √144 = 12 дюймів. - Обчислюємо площу:
S = 5 дюймів × 12 дюймів = 60 дюймів².
Обчислення через периметр та одну сторону
Периметр (P) — це сума довжин усіх сторін прямокутника: P = 2 × (a + b). Якщо вам відомий периметр та одна зі сторін (наприклад, a), ви легко можете знайти другу сторону (b).
Приклад:
Периметр земельної ділянки становить 30 метрів, а її довжина — 10 метрів. Яка її площа?
- Знаходимо ширину:
30 = 2 × (10 + b)
15 = 10 + b
b = 5 метрів. - Обчислюємо площу:
S = 10 м × 5 м = 50 м².
Практичне застосування знань: таблиця прикладів
Щоб закріпити розуміння, розглянемо кілька типових геометричних задач.
| Відомі дані | Що потрібно знайти | Кроки розв’язання | Результат |
|---|---|---|---|
| Довжина = 8 см, Ширина = 4 см | Площа (S) | S = 8 × 4 | S = 32 см² |
| Діагональ = 10 м, Сторона (a) = 6 м | Площа (S) | 1. Знайти сторону b: b = √(10² – 6²) = √64 = 8 м 2. Знайти площу: S = 6 × 8 | S = 48 м² |
| Периметр = 28 см, Сторони співвідносяться як 3:4 | Площа (S) | 1. Позначимо сторони як 3x і 4x. 2. P = 2 × (3x + 4x) = 14x = 28. x=2. 3. a = 6 см, b = 8 см. S = 6 × 8 | S = 48 см² |
| Площа = 72 м², Довжина вдвічі більша за ширину | Довжина та ширина | 1. Позначимо ширину як x, довжину як 2x. 2. S = x × 2x = 2x² = 72. x² = 36. x=6. 3. a=12 м, b=6 м | Ширина 6 м, довжина 12 м |
Підсумовуючи ключові ідеї
Знаходження площі прямокутника — це базове вміння, що відкриває двері до вирішення багатьох практичних та теоретичних завдань. Незалежно від того, чи маєте ви справу з ремонтом, плануванням ділянки, чи просто розв’язуєте геометричні задачі, головне — чітко розуміти, які дані у вас є, та яку формулу краще застосувати.
Пам’ятайте про основний принцип: площа — це добуток довжини на ширину. А якщо ці параметри невідомі, завжди можна знайти обхідний шлях через діагональ, периметр або інші властивості цієї простої, але важливої фігури. Сподіваємось, цей посібник допоміг вам освіжити знання та додав упевненості у власних силах.